モンティ・ホール問題 というのがある。 アメリカのゲームショー番組の中で行われた以下のようなゲームに関する問題である。
- 三つのドアのどれか一つの後ろに当たりの商品が隠されている。残りの二つはハズレだ。
- プレイヤーである番組参加者は、一つのドアを選ぶ。
- 番組司会者のモンティは、残り二つのドアのうちからハズレのドアを一つ開けて見せる。
- モンティはプレイヤーに「ドアを選びなおしても良い」と言う。
- プレイヤーはドアを選びなおすべきだろうか?

当たりはどれか一つ。
この問題の正解は、「選びなおした方が良い。何故なら当たる確率が倍になるから」というものだ。
しかし、これを正解とするということに納得しない人が多いらしい。直感と異なるからだ。
教授レベルの数学者を含む多くの人が反論したらしい。
大きな論争となったこの問題は、結局コンピューター上でのシミュレーションで決着がついたそうだ。
とても興味深い題材なので、私も C# でシミュレーションをやってみた。
// モンティ・ホール問題 - Wikipedia
// http://ja.wikipedia.org/wiki/%E3%83%A2%E3%83%B3%E3%83%86%E3%82%A3%E3%83%BB%E3%83%9B%E3%83%BC%E3%83%AB%E5%95%8F%E9%A1%8C
using System;
using System.Linq;
namespace モンティ・ホール問題
{
static class プログラム
{
static void Main(string[] コマンドライン引数)
{ シミュレーター.シミュレート(コマンドライン引数から繰り返し回数を得る(コマンドライン引数)); }
static int コマンドライン引数から繰り返し回数を得る(string[] コマンドライン引数)
{
if (コマンドライン引数.Length < 0)
{
int 繰り返し回数;
if (int.TryParse(コマンドライン引数[0], out 繰り返し回数))
return 繰り返し回数;
}
const int デフォルトの繰り返し回数 = 1000000;
return デフォルトの繰り返し回数;
}
}
static class シミュレーター
{
public static void シミュレート(int 試す回数)
{ 結果.表示(選びなおす場合に当たる確率: シミュレート(試す回数, 選びなおす: true),
選びなおさない場合に当たる確率: シミュレート(試す回数, 選びなおす: false)); }
static double シミュレート(int 試す回数, bool 選びなおす)
{
var 当たりの回数 = Enumerable.Range(1, 試す回数).Count(_ =< ゲーム.プレイする(選びなおす));
var 当たる確率 = (double)当たりの回数 / 試す回数;
結果.表示(選びなおす, 試す回数, 当たりの回数, 当たる確率);
return 当たる確率;
}
static class 結果
{
public static void 表示(double 選びなおす場合に当たる確率, double 選びなおさない場合に当たる確率)
{ 表示(選びなおす場合と選びなおさない場合の当たる確率の比:
選びなおす場合に当たる確率 / 選びなおさない場合に当たる確率); }
public static void 表示(double 選びなおす場合と選びなおさない場合の当たる確率の比)
{ Console.WriteLine("・結論: 選びなおす場合は、選びなおさない場合に比べて、{0} 倍当たりやすい。",
選びなおす場合と選びなおさない場合の当たる確率の比); }
public static void 表示(bool 選びなおした, int 試した回数, int 当たった回数, double 当たる確率)
{ Console.WriteLine("・{0}場合は、当たりの回数は: {1} 回中 {2} 回で、当たる確率は {3}。",
選びなおした ? "選びなおした" : "選びなおさなかった", 試した回数, 当たった回数, 当たる確率); }
}
}
static class ゲーム
{
const int 全ドアの数 = 3;
public static bool プレイする(bool 選びなおす)
{
var 当たりのドア = ランダムなドア();
var プレイヤーが選択したドア = ランダムなドア();
var モンティの開けたドア = 残りのドアから一つ(当たりのドア, プレイヤーが選択したドア);
if (選びなおす)
プレイヤーが選択したドア
= 残りのドアから一つ(プレイヤーが選択したドア, モンティの開けたドア);
return プレイヤーが選択したドア == 当たりのドア;
}
static int 残りのドアから一つ(int 当たりのドア, int プレイヤーが選択したドア)
{
return 当たりのドア == プレイヤーが選択したドア
? 残りのドアからランダムに一つ(除外するドア: 当たりのドア)
: 残りのドアからどれでも一つ(一つ目の除外するドア: 当たりのドア,
二つ目の除外するドア: プレイヤーが選択したドア);
}
static int 残りのドアからランダムに一つ(int 除外するドア)
{ return 或るドアから数えてX番目のドア(除外するドア,
そのドアから数えてX番目: ランダム.一から或る数までの乱数(全ドアの数 - 1)); }
static int 或るドアから数えてX番目のドア(int 或るドア, int そのドアから数えてX番目)
{ return (或るドア + そのドアから数えてX番目) % 全ドアの数; }
static int 残りのドアからどれでも一つ(int 一つ目の除外するドア, int 二つ目の除外するドア)
{ return Enumerable.Range(0, 全ドアの数)
.First(ドア =< ドア != 一つ目の除外するドア && ドア != 二つ目の除外するドア); }
static int ランダムなドア()
{ return ランダム.零から或る数までの乱数(全ドアの数); }
}
static class ランダム
{
static readonly Random 乱数 = new Random();
public static int 零から或る数までの乱数(int 或る数)
{ return 乱数.Next(或る数); }
public static int 一から或る数までの乱数(int 或る数)
{ return 乱数.Next(或る数) + 1; }
}
}
以下のように正解の通りの結果となった。
- 選びなおした場合は、当たりの回数は: 1000000 回中 666662 回で、当たる確率は 0.666662。
- 選びなおさなかった場合は、当たりの回数は: 1000000 回中 333802 回で、当たる確率は 0.333802。
- 結論: 選びなおす場合は、選びなおさない場合に比べて、1.99717796777731 倍当たりやすい。
実は、プログラムを書いていく過程で、問題が整理されていったため、途中から実行する迄もなく結果は明白なように感じていた。
以下のように考えたのだ。
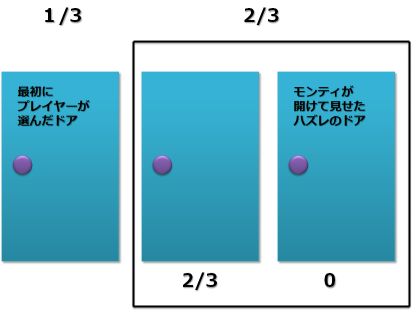
- 最初にプレイヤーがドアを選んだ時点で、そのドアが当たりである確率は、1/3 だ。
- そのとき、プレイヤーが選ばなかった残りの二つのドアが当たりである確率も、それぞれ 1/3 だ。
- 即ち、残りの二つのドアのどちらかが当たりである確率は 2/3。
- つまり、「残りの二つのドアのどちらかが当たりである確率」は「プレイヤーが最初に選んだドアが当たりである確率」の倍。
- ところが、モンティは、「残り二つのドアのどちらがハズレか」を必ず教えてくれる。
- 残りの二つのドアのどちらかが当たりである確率は 2/3 だが、残りの二つのドアのうちモンティが開けて見せた方が当たりである確率は 0 で、残りの二つのドアのうちモンティが開けなかった方が当たりである確率は 2/3。
- 残りの二つのドアのうちモンティが開けなかった方を選びなおした方が、当たる確率が倍、ということだ。
ちなみに、このゲームの「番組司会者のモンティは、残り二つのドアのうちからハズレのドアを一つ開けて見せる。」の部分で、プレイヤーから見て、「(プレイヤーの最初の選択が当たりかハズレかによって) モンティにはハズレのドアを一つ開けて見せないという選択もあったのではないか」と疑われる場合は、上記確率の計算の話は成り立たないと思う。
あくまで、プレイヤーから見て、モンティが (プレイヤーの最初の選択に関わらず) 必ずハズレのドアを一つ開けて見せる場合の話。