[Event] Windows Developer Days

| 『Windows Developer Days』 | |
|---|---|
| 日時 | 2012年4月24日(火)~25日(水) 10:00-18:00 |
| 会場 | ザ・プリンスパークタワー東京 |
| 参加費 | ¥84,000 (早期割引 4月18日 16:59 迄 税込¥63,000) |
| 詳細/参加登録 | Windows Developer Days |
« 2012年03月 | メイン | 2012年05月 »

| 『Windows Developer Days』 | |
|---|---|
| 日時 | 2012年4月24日(火)~25日(水) 10:00-18:00 |
| 会場 | ザ・プリンスパークタワー東京 |
| 参加費 | ¥84,000 (早期割引 4月18日 16:59 迄 税込¥63,000) |
| 詳細/参加登録 | Windows Developer Days |
モンティ・ホール問題 というのがある。 アメリカのゲームショー番組の中で行われた以下のようなゲームに関する問題である。
- 三つのドアのどれか一つの後ろに当たりの商品が隠されている。残りの二つはハズレだ。
- プレイヤーである番組参加者は、一つのドアを選ぶ。
- 番組司会者のモンティは、残り二つのドアのうちからハズレのドアを一つ開けて見せる。
- モンティはプレイヤーに「ドアを選びなおしても良い」と言う。
- プレイヤーはドアを選びなおすべきだろうか?

当たりはどれか一つ。
この問題の正解は、「選びなおした方が良い。何故なら当たる確率が倍になるから」というものだ。
しかし、これを正解とするということに納得しない人が多いらしい。直感と異なるからだ。
教授レベルの数学者を含む多くの人が反論したらしい。
大きな論争となったこの問題は、結局コンピューター上でのシミュレーションで決着がついたそうだ。
とても興味深い題材なので、私も C# でシミュレーションをやってみた。
// モンティ・ホール問題 - Wikipedia
// http://ja.wikipedia.org/wiki/%E3%83%A2%E3%83%B3%E3%83%86%E3%82%A3%E3%83%BB%E3%83%9B%E3%83%BC%E3%83%AB%E5%95%8F%E9%A1%8C
using System;
using System.Linq;
namespace モンティ・ホール問題
{
static class プログラム
{
static void Main(string[] コマンドライン引数)
{ シミュレーター.シミュレート(コマンドライン引数から繰り返し回数を得る(コマンドライン引数)); }
static int コマンドライン引数から繰り返し回数を得る(string[] コマンドライン引数)
{
if (コマンドライン引数.Length < 0)
{
int 繰り返し回数;
if (int.TryParse(コマンドライン引数[0], out 繰り返し回数))
return 繰り返し回数;
}
const int デフォルトの繰り返し回数 = 1000000;
return デフォルトの繰り返し回数;
}
}
static class シミュレーター
{
public static void シミュレート(int 試す回数)
{ 結果.表示(選びなおす場合に当たる確率: シミュレート(試す回数, 選びなおす: true),
選びなおさない場合に当たる確率: シミュレート(試す回数, 選びなおす: false)); }
static double シミュレート(int 試す回数, bool 選びなおす)
{
var 当たりの回数 = Enumerable.Range(1, 試す回数).Count(_ =< ゲーム.プレイする(選びなおす));
var 当たる確率 = (double)当たりの回数 / 試す回数;
結果.表示(選びなおす, 試す回数, 当たりの回数, 当たる確率);
return 当たる確率;
}
static class 結果
{
public static void 表示(double 選びなおす場合に当たる確率, double 選びなおさない場合に当たる確率)
{ 表示(選びなおす場合と選びなおさない場合の当たる確率の比:
選びなおす場合に当たる確率 / 選びなおさない場合に当たる確率); }
public static void 表示(double 選びなおす場合と選びなおさない場合の当たる確率の比)
{ Console.WriteLine("・結論: 選びなおす場合は、選びなおさない場合に比べて、{0} 倍当たりやすい。",
選びなおす場合と選びなおさない場合の当たる確率の比); }
public static void 表示(bool 選びなおした, int 試した回数, int 当たった回数, double 当たる確率)
{ Console.WriteLine("・{0}場合は、当たりの回数は: {1} 回中 {2} 回で、当たる確率は {3}。",
選びなおした ? "選びなおした" : "選びなおさなかった", 試した回数, 当たった回数, 当たる確率); }
}
}
static class ゲーム
{
const int 全ドアの数 = 3;
public static bool プレイする(bool 選びなおす)
{
var 当たりのドア = ランダムなドア();
var プレイヤーが選択したドア = ランダムなドア();
var モンティの開けたドア = 残りのドアから一つ(当たりのドア, プレイヤーが選択したドア);
if (選びなおす)
プレイヤーが選択したドア
= 残りのドアから一つ(プレイヤーが選択したドア, モンティの開けたドア);
return プレイヤーが選択したドア == 当たりのドア;
}
static int 残りのドアから一つ(int 当たりのドア, int プレイヤーが選択したドア)
{
return 当たりのドア == プレイヤーが選択したドア
? 残りのドアからランダムに一つ(除外するドア: 当たりのドア)
: 残りのドアからどれでも一つ(一つ目の除外するドア: 当たりのドア,
二つ目の除外するドア: プレイヤーが選択したドア);
}
static int 残りのドアからランダムに一つ(int 除外するドア)
{ return 或るドアから数えてX番目のドア(除外するドア,
そのドアから数えてX番目: ランダム.一から或る数までの乱数(全ドアの数 - 1)); }
static int 或るドアから数えてX番目のドア(int 或るドア, int そのドアから数えてX番目)
{ return (或るドア + そのドアから数えてX番目) % 全ドアの数; }
static int 残りのドアからどれでも一つ(int 一つ目の除外するドア, int 二つ目の除外するドア)
{ return Enumerable.Range(0, 全ドアの数)
.First(ドア =< ドア != 一つ目の除外するドア && ドア != 二つ目の除外するドア); }
static int ランダムなドア()
{ return ランダム.零から或る数までの乱数(全ドアの数); }
}
static class ランダム
{
static readonly Random 乱数 = new Random();
public static int 零から或る数までの乱数(int 或る数)
{ return 乱数.Next(或る数); }
public static int 一から或る数までの乱数(int 或る数)
{ return 乱数.Next(或る数) + 1; }
}
}
以下のように正解の通りの結果となった。
- 選びなおした場合は、当たりの回数は: 1000000 回中 666662 回で、当たる確率は 0.666662。
- 選びなおさなかった場合は、当たりの回数は: 1000000 回中 333802 回で、当たる確率は 0.333802。
- 結論: 選びなおす場合は、選びなおさない場合に比べて、1.99717796777731 倍当たりやすい。
実は、プログラムを書いていく過程で、問題が整理されていったため、途中から実行する迄もなく結果は明白なように感じていた。
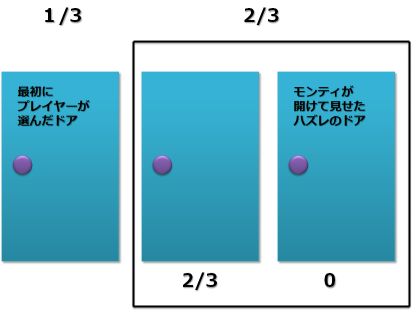
以下のように考えたのだ。
SyntaxHighlighter を使って C++ のソースコードに色を付けてみる実験。
// MFC版
// ドキュメントの内容を:
// ・クリップボードへメタファイルと独自形式でコピー
// ・クリップボードから独自形式でペースト
// ※ MyDocument::Serialize と MyView::OnDraw でのドキュメントの描画を実装しておくこと
// MyView.h
class MyView : public CView
{
DECLARE_DYNCREATE(MyView)
DECLARE_MESSAGE_MAP()
HGLOBAL globalMemoryHandle;
protected:
MyView() : globalMemoryHandle(NULL)
{}
MyDocument* GetDocument() const
{ return reinterpret_cast<MyDocument*>(m_pDocument); }
virtual void OnDraw(CDC* pDC)
{
if (GetDocument() != NULL)
/* ドキュメントの描画 */ ;
}
afx_msg void OnEditCopy()
{
if (GetDocument() == NULL)
return;
// ドキュメントが空なら何もしない
// 例.
// if (GetDocument()->IsEmpty())
// return;
// 拡張メタファイルの作成
CClientDC clientDC(this);
CMetaFileDC metaDC;
metaDC.CreateEnhanced(&clientDC, NULL, NULL, NULL);
OnDraw(&metaDC);
const HENHMETAFILE enhancedMetaFileHandle = metaDC.CloseEnhanced();
// メモリへのシリアライズ
CSharedFile sharedFile;
{
CArchive ar(&sharedFile, CArchive::store);
GetDocument()->Serialize(ar);
}
globalMemoryHandle = sharedFile.Detach();
// クリップボードへの書き込み
if (OpenClipboard()) {
::EmptyClipboard();
::SetClipboardData(CF_ENHMETAFILE, CopyEnhMetaFile(enhancedMetaFileHandle, NULL));
::SetClipboardData(CF_PRIVATEFIRST, globalMemoryHandle);
::CloseClipboard();
}
::DeleteEnhMetaFile(enhancedMetaFileHandle);
}
afx_msg void OnEditPaste()
{
if (GetDocument() == NULL)
return;
if (OpenClipboard()) {
const HANDLE clipboardData = ::GetClipboardData(CF_PRIVATEFIRST);
if (clipboardData != NULL) {
CSharedFile sharedFile;
sharedFile.SetHandle(clipboardData);
{
CArchive ar(&sharedFile, CArchive::load);
GetDocument()->Serialize(ar);
}
sharedFile.Detach();
GetDocument()->SetModifiedFlag();
Invalidate();
}
::CloseClipboard();
}
}
afx_msg void OnDestroyClipboard()
{
CView::OnDestroyClipboard();
// WM_DESTROYCLIPBOARD 時に CF_PRIVATEFIRST で確保したメモリを開放する必要がある
if (globalMemoryHandle != NULL) {
::GlobalUnlock(globalMemoryHandle);
::GlobalFree (globalMemoryHandle);
globalMemoryHandle = NULL;
}
}
};
// MyView.cpp
#include "MyView.h"
IMPLEMENT_DYNCREATE(MyView, CView)
BEGIN_MESSAGE_MAP(MyView, CView)
ON_COMMAND(ID_EDIT_COPY, OnEditCopy)
ON_COMMAND(ID_EDIT_PASTE, OnEditPaste)
ON_WM_DESTROYCLIPBOARD()
END_MESSAGE_MAP()